728x90
그래프 (Grpah)
함수 그래프 != 그래프 이론의 그래프
- 함수 그래프 : x(정의역), y(치역)에 해당하는 값을 좌표 상에 표시하는것
- 그래프 이론의 그래프 : *꼭짓점(Vertex)과 간선(Edge)으로 구성, G = (V, E)
*꼭짓점(Vertex) == 노드(Node)
+추가
- 그래프에는 간선이 화살표 => 단방향, 실선인 경우 => 양방향 그래프
- 간선에 가중치를 주는 경우도 있음, 아무것도 쓰여있지 않으면 모두 1이거나 같은 가중치
깊이 우선 탐색 (DFS, Depth-first Search)
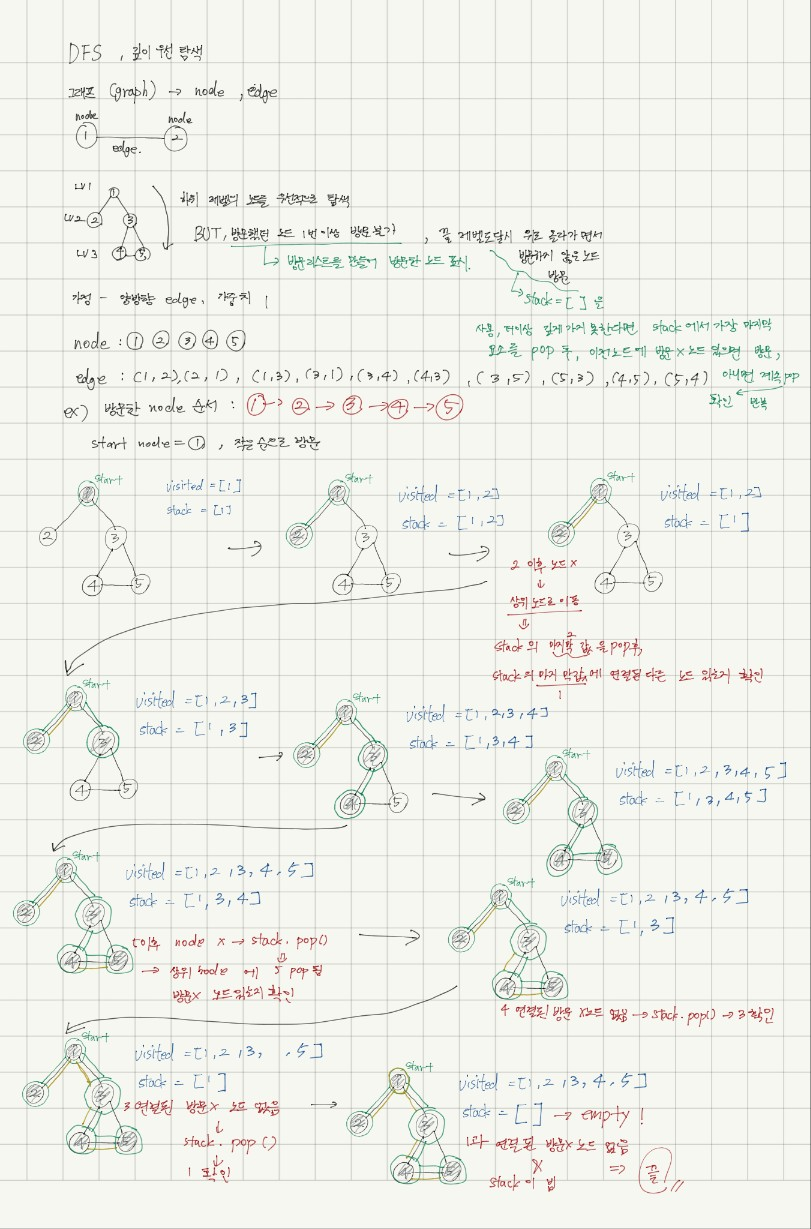
: 말 그대로 상위 레벨의 노드 --> 하위 레벨의 노드를 우선적으로 탐색하는 것이다. 하지만 이미 방문했던 노드는 다시 방문하지 못하며 더이상 탐색할 노드가 없을 시 이전 노드로 옮겨서 방문하지 않은 다른 연결된 노드가 있다면 그 노드를 방문하고 그렇지 않다면 '이전노드로 거슬러 올라가기 -> 다른 연결된 노드가 있는지 확인' 과정을 시작 노드에 도달해서 더이상 탐색할 노드가 없을 때까지 반복한다.
- 인접행렬 or 인접리스트 -> 노드, 엣지의 정보가 들어있음
- 방문 확인 리스트 -> 노드를 방문 했다면 해당 노드를 방문 확인 리스트에 추가
- 스택 -> 방문하지 않은 노드를 append, 더이상 깊게 탐색 불가하면 가장 마지막 노드를 pop
=> 탐색이 끝나면 빈 스택됨
**항상 같은 결과를 내기 위해서 여기에서는 노드를 오름차순으로 방문하였음**

수행 단계
노드와 간선의 정보를 인접행렬 or 인접 리스트에 저장
빈 방문리스트, 스택 정의시작 노드를 스택에 append, 방문처리
while 스택이 차 있음
if 스택[-1]에 방문x 연결된 노드 존재o
-> 시작 노드에서 연결된 방문하지 않은 노드로 이동
-> 방문처리
for i in 현재 노드에 연결된 노드들:
if 방문x노드
스택에 추가 -> break
if i가 방문 한 노드라면:
-> 스택.pop()
파이썬 코드 - 스택 사용
def dfs(graph, start):
visited = [] # 방문 확인 그래프
stack = [] # 스택
# 시작노드를 스택에 추가, 방문처리
stack.append(start)
visited.append(start)
# 스택이 비면 종료
while stack:
node = stack[-1] # 현재 노드
if node not in visited: # 현재 노드가 방문x 노드이면
visited.append(node) # 방문처리
for i in graph[node]: # 현재 노드와 연결된 방문x 않은 노드 탐색
if i not in visited: # 방문x 노드가 있으면 스택에 추가
stack.append(i)
break
if i in visited: # 현재노드와 연결된 노드가 없는 경우
stack.pop() # 스택의 마지막 pop
return visited
graph = [[],[2,3],[1],[1,4,5],[3,5],[4,3]]
# 오름차순으로 방문하기 위한 정렬
for edge in graph:
edge.sort()
res = dfs(graph, 1)
print(res)
파이썬 코드 - 재귀 사용
def dfs(graph, node, visited):
visited.append(node)
print(node)
for i in graph[node]: # 현재 노드와 연결된 노드 탐색
if i not in visited: # 방문x 노드가 있다면 dfs함수 호출
dfs(graph, i, visited)
graph = [[],[2,3],[1],[1,4,5],[3,5],[4,3]]
visited = []
# 오름차순으로 방문하기 위한 정렬
for edge in graph:
edge.sort()
dfs(graph, 1, visited)728x90
반응형
'Data structure & Algorithm' 카테고리의 다른 글
| [Algorithm] 너비 우선 탐색 (BFS, Breadth-first Search) (2) | 2024.01.25 |
|---|---|
| [Data structure] 스택(Stack), 큐(Queue) (1) | 2024.01.11 |
| [Algorithm] 그리디 알고리즘 (Greedy Algorithm) (2) | 2024.01.09 |
| [Algorithm] 이분탐색 (Binary Search) - 변형 (0) | 2024.01.04 |
| [Algorithm] 최대공약수 (0) | 2023.12.25 |