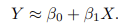notty

RSS의 비율이 적은 모델이 더 설명력이 있음 -> R^2지표의 원리 R^2 = (TSS - RSS) / TSS = 1 - (RSS / TSS) = ESS / TSS : 총 제곱합 중 설명된 체곱합의 비율 * y의 평균 : 종속변수의 평균은 해당 변수의 전반적인 중심 경향을 보이기 때문에 이를 통해 해당 변수의 변동성을 이해할 수 있음. TSS (총 제곱합, Total Sum of Square) 실제값과 y 평균값의 차이 : 종속변수 y의 총 변동량 RSS (잔차 제곱합, Residual Sum of Square) 회귀모델의 예측값과 실제값의 차이 : 회귀모델이 설명하지 못하는 오차 하이퍼 파리미터 조정, 다른 모델 선택 등으로 줄일 수 있음 -> 하지만 RSS말고 다른 요소들도 고려 필요 ESS (설명..

*에러 : 분산에 의한, 편향에 의한, 축소 불가능한 에러 이상적인 모델 : 분산이 작고 편향이 작은 robust한 모델 모델의 분산 (variance) : 해당 모델을 다른 훈련 데이터로 학습시키는 경우 f^이 달라지는 정도 모델의 복잡도와 관련이 있다. 분산이 높다 -> 모델이 훈련데이터에 overfitting 되어있다 => 모델이 과하게 복잡함 분산이 낮다 -> 모델의 복잡도가 적절하다. 그래프 유연한 모델일수록 MSE가 작아진다. 어느정도 유연해지면 그 이후는 MSE증가한다. 모델의 편향 (bias) : 복잡한 상관관계를 가지는 데이터를 덜복잡한 모델에 근사했을 경우 생기는 에러 데이터의 상관성과 연관되어있다 (얘를 들어, 현실의 데이터를 선형회귀에 근사하면 차이가 존재한다) 편향이 높다 : 선택..

**참고  Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani. An Introduction to Statistical Learning : with Applications in R. New York :Springer, 2013.선형회귀 주로 양적 반응변수를 예측많은 통계학습 방법의 기반1. 단순선형회귀: 하나의 설명변수(X)로 Y를 예측한다 (X와 Y사이에 선형적 상관관계가 있다고 가정) ~ : '근사적으로 모델링 된'을 의미β0 : 알려지지 않은 상수, 절편(intercept)β1 : 알려지지 않은 상수, 기울기 추정식ŷ  : X = x 일때 Y의 예측값(추정값)ˆβ0, ˆβ1 : 예측된 β0, β11..

일반적인 형태Y = f(X)+εf : 알려지지 않은 고정함수Y : 종속변수, 결과변수 등등X : 독립변수, 설명변수 등등ε : 랜덤 오차항 (X와 독립적, 평균 = 0) 1. 통계학습이란?: f를 추정하는 일련의 기법들을 말한다 1.1 f를 추정하는 이유는?: 대표적으로 예측과 추론을 수행하기 위함 예측(Prediction) -> 축소가능 오차를 최소로 하는 f를 추정하는 것이 목표 Ŷ = f̂(X)ε 의 평균이 0이어서 생략f̂  : 블랙박스로 취급 한다. f̂ 이 Y에 대한 정확한 예측을 수행한다면 모델의 형태에는 신경쓰지 않는다예측 정확성축소가능(reducible) 오차 : f를 다시 추정해나가면서 개선 가능축소불가능(irreducible) 오차 : 개선 ..