728x90
Single Layer Neural Network
: 히든 레이어 = 1인 NN
구조
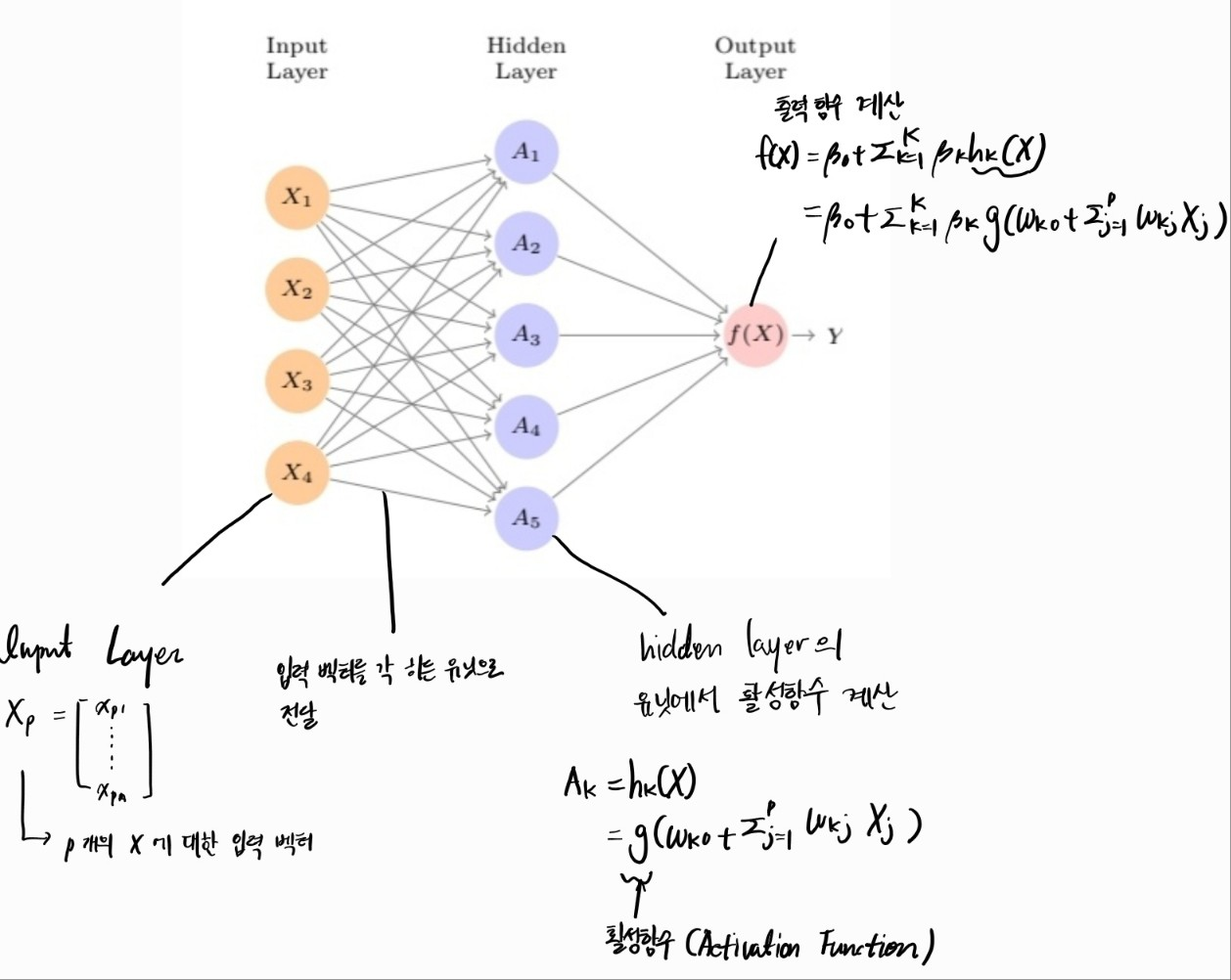
- 입력층 - 출력층 이외에 hidden layer이 존재한다. 입력 층의 각 노드와 히든층의 각 노드가 완전 연결 되어
- Hidden layer : 입력층의 선형 결합을 더하고 활성함수를 계산하여 출력노드로 전달한다.

- Output layer : 출력 함수를 적용하여 최종 Y를 결정한다. 이 때 출력 층의 유닛의 개수는 문제에 따라서 달라진다. 예를 들어 multi calss calssification의 경우 softmax함수를 사용하고 출력 층을 class의 개수 만큼 설정 반면하는 반면 회귀 문제의 경우 출력 함수를 항등함수로 설정하여 마지막 히든 레이어의 신호를 그대로 전달한다.
- Single Layer Neural Network의 hidden unit수를 조절하면 더 복잡한 문제도 해결이 가능하지만 히든레이어를 늘리면 더 효과적으로 해결 가능 --> Multi Layer NN
Multi Layer Neural Network
: 히든 레이어 >= 2인 NN

활성화함수 (Activation Function)
: 신경망이 복잡한 비선형 관계를 학습할 수 있게 해주며, 네트워크의 출력을 결정짓는 역할을 한다.
- 인간의 뇌를 예로 들면 인간의 생각, 감정, 행동 등을 조절하는 것과 유사하다.
- 비선형 (non-linear)함수를 사용한다. (선형함수를 사용하는 경우 비선형적 관계를 학습하지 못함)
** 선형함수를 사용하지 않는 이유 : 선형 함수를 사용하여 은닉층을 여러 번 추가한다고 해도 그 결과는 하나의 선형 함수를 추가한 것과 큰 차이가 없다. 예를 들어 4개의 층에 활성 함수로 선형 함수를 사용한다면 f(X) = W^4X이다. 이는 여전히 선형 함수이며 비선형 관계를 학습하지 못한다.
활성화 함수의 종류

- Sigmoid
- x에 대해 0과 1사이의 값을 가진다
- 시그모이드를 미분하면 최대 0.25의 값을 가지는데 이는 역전파 적용하여 가중치를 업데이트하는 과정 활성함수 미분값이 반복으로 곱해지는데 이 때 기울기가 빠르게 소실될 수 있는 문제가 있다. (기울기 소실 문제, Gradient Vanishing Problem)
- tanh (Hyperbolic Tangent)
- x에 대해 -1과 1사이의 값을 가진다.
- 미분하면 최대 1이기 때문에 시그모이드보다 기울기 소실의 문제가 개선되었다. 하지만 여전히 0이 아닐 때의 기울기는 곱해질수록 작아지기 때문에 기울기 소실 문제는 남아있다. (기울기 소실 문제, Gradient Vanishing Problem)
- ReLU (Rectified Linear Unit)
- if x > 0 y =x, else 0
- 0보다 큰 양수의 경우 기울기 1을 가지기 떄문에 기울기 소실 문제를 해결할 수 있다. 하지만 x가 0보다 작은 경우 미분값이 0으로 해당 뉴런이 비활성화 되는 문제가 발생한다.
- Leaky ReLU (Leaky Rectified Linear Unit)
- if x >= 0 y=x, else y = αx
α : 작은값 (예: α = 0.001) - x < 0 경우 작은 기울기를 부여하여 역전파 알고리즘 작동시 뉴런이 비활성화 되는것을 방지한다.
- if x >= 0 y=x, else y = αx
출력함수
- 이진분류 : sigmoid, softmax
- 다중 클래스 분류 : softmax
- 회귀 : 항등함수
과적합 방지
- Ridge regulation(L2 norm)
- Dropout
손실함수
- 분류 : cross entropy
- 회귀 : MSE 등등
728x90
반응형
'통계 > ISLP' 카테고리의 다른 글
| [ISLP Chapter 10] CNN (1) | 2024.05.01 |
|---|---|
| [ISLP Chapter 9] 서포트 벡터 머신 (0) | 2024.04.22 |
| [ISLP Chapter 9] 서포트 벡터 분류기 (0) | 2024.03.20 |
| [ISLP Chapter 7] 조각별 다항식 회귀 (Piecewise polynomial regression) (0) | 2024.03.09 |
| [ISLP Chapter 7] 기저함수 (0) | 2024.03.06 |