728x90
기저함수란?
- 공간상에서 일어나는 운동을 표현하기 위한 기본적인 함수들의 집합이고 그것을 이용해서 공간상에서 일어나는 모든 운동을 표현할 수 있음. (https://www.gpgstudy.com/forum/viewtopic.php?highlight=&t=2728)
- 기저함수는 특정한 규칙에 따라 만들어지는 함수의 열(sequence)로서 충분히 많은 수의 함수가 있으면 어떤 모양의 함수라도 비슷하게 흉내낼 수 있는 것을 말한다. (https://datascienceschool.net/03%20machine%20learning/06.02%20%EA%B8%B0%EC%A0%80%ED%95%A8%EC%88%98%20%EB%AA%A8%ED%98%95%EA%B3%BC%20%EA%B3%BC%EC%B5%9C%EC%A0%81%ED%99%94.html)
- 선형대수에서의 기저(basis)는 서로 독립이면서 주어진 공간 전체를 표현할 수 있는 벡터
- 기저(basis) : 밑받침이 되는 부분
- 그럼 통계에서의 기저함수는??????? 함수를 이루는 밑받침이 되는 함수?????그럼 서로 독립적이면서
- 함수 공간 형성: 기저 함수들은 함께 조합되어 특정 종류의 함수를 만들기 위한 공간을 형성
- 다른 함수 표현 및 근사: 기저 함수들은 다른 함수를 나타내는 데 사용되며 특정 함수를 나타내기 위해 기저 함수들의 조합을 사용할 수 있음

- bK(xi), 기저함수를 설명변수로 가지는 표준모델
- 이전까지 본 다항식 회귀, 계단함수를 사용한 회귀 모두 기저함수의 특별한 경우임
- 최소제곱 적합 가능

- 상수함수를 기저함수로 사용하는 모델
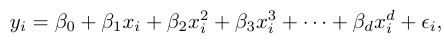
- 다항식 함수를 기저함수로 사용하는 모델

- 조각별 상수함수를 기저함수로 사용하는 모델
728x90
반응형
'통계 > ISLP' 카테고리의 다른 글
| [ISLP Chapter 9] 서포트 벡터 분류기 (0) | 2024.03.20 |
|---|---|
| [ISLP Chapter 7] 조각별 다항식 회귀 (Piecewise polynomial regression) (0) | 2024.03.09 |
| [ISLP Chapter 7] 계단함수 (0) | 2024.03.06 |
| [ISLP Chapter 7] 다항식 회귀 (0) | 2024.03.05 |
| [ISLP Chapter 4] 분류 (1) | 2024.02.13 |