728x90
최적의 초평면을 찾아보자!!
초평면(Hyperplane)
: 주어진 차원보다 한 차원 낮은 아핀(affine)부분공간을 의미한다
ex) p차원 --> (p-1)차원의 초평면을 갖는다, 2차원 --> 1차원의 초평면을 갖는다
하지만 클래스를 분류하는 초평면은 무수히 많음...
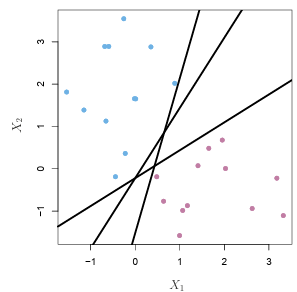
--> 마진을 최대로 하는 최적의 초평면을 찾자 ==> 최대 마진 분류기
* 마진(Margine) : 서포트벡터와 초평면과의 수직거리

최대 마진 분류기(Maximum margin classifier) => 하드 마진(Hard margin)
: 마진을 최대로 하는 초평면
- 관측치들과 분류 초평면의 거리를 계산하는데 이떄의 관측치는 서포트 벡터를 의미한다
--> 최대마진 초평면은 서포트 벡터에 직접적으로 의존적이다 (거리 계산시 서포트 베터만 사용하여 연산량 작아짐, 하지만 서포트 벡터를 찾는 과정을 고려한다면 크게 연산량이 적어지지는 않음) 
- (9.9) M(margin)을 최대로 하는 파라미터(베타)를 찾는것이 목표
- (9.10) 제약
모든 파라미터 제곱의 합은 1 - (9.11) 제약
M이 양수이면 각 관측치가 초평면의 올바른 쪽에 존재할것을 보장한다.
하지만
- 최대 마진 분류기는 완벽하게 분류되지 않는 경우에 M>0에서 해가 존재하지 않는다. (완벽분류x => M은 음수)
- 훈련데이터에 대해서 과적합(분산이 커진다)
--> 오차를 어느정도 허용하는 초평면을 사용한다 ==> 소프트 마진(Sofㅅ margin)
소프트 마진(Soft margin)
: 오차를 허용하는 정도를 조절
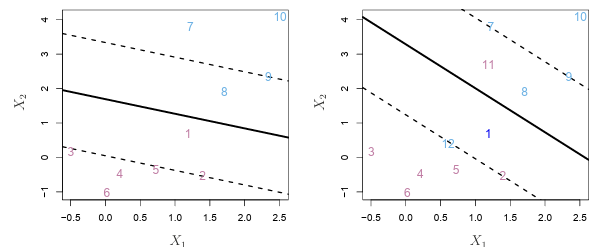
- 왼쪽 그림
㉮ 3, 4, 5, 6 / 7, 10은 마진의 올바른 곳에 있다 ( εi = 0 )
㉯ 2 / 9는 마진상에 있다 ( εi = 0 )
㉰ 1 / 8은 마진의 옳지 않은 쪽에 있다 ( εi > 0 ) - 오른쪽 그림 (왼쪽 그림에 11, 12 포인트를 추가함)
㉮ 3, 4, 5, 6 / 7, 10은 마진의 올바른 곳에 있다 ( εi = 0 )
㉯ 2 / 9는 마진상에 있다 ( εi = 0 )
㉰ 1 / 8은 마진의 옳지 않은 쪽에 있다 ( εi > 0 )
㉱ 11 / 12 초평면의 옳지 않은 쪽에 있다 ( εi > 1 )
- 왼쪽 그림
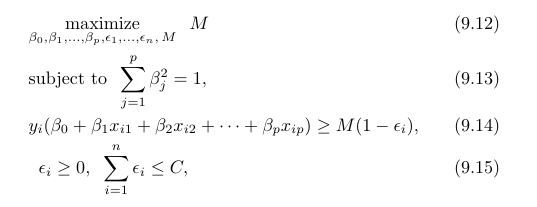
- ε : 개별 관측치들이 초평면의 옳지 않은 곳에 있을 수 있ㄱ 하는 슬랙변수(slack variable)
- εi = 0 : 마진의 올바른 쪽에 있
- εi > 0 : i 번째 관측치는 마진의 옳지 않은 쪽에 있다
- εi > 1 : 관측치는 초평면의 옳지 않은 쪽에 있다
- 조율파라미터(C) : 허용될 위반의 수와 그 정도를 결정, cv를 통해 최적의 값을 찾는다
- 오차( ε )의 합을 한정
- C = 0 : 오차를 허용하지 않는다
- C > 0 : 초평면의 옳지 않은 쪽에 있을 수 있음
- C에 따른 편향(bias)-분산(variance) 절충
- C가 큰 경우 -> 마진 넓 -> 허용오차 많아짐 -> 분산 낮아짐, 편향 증가
* 서포트 벡터가 많아짐 - C가 작은 경우 -> 마진 좁 -> 허용오차 적어짐(모델이 데이터에 고도로 적합) -> 분산 높아짐, 편향 감소
*서포트 벡터가 적어짐
- C가 큰 경우 -> 마진 넓 -> 허용오차 많아짐 -> 분산 낮아짐, 편향 증가
728x90
반응형
'통계 > ISLP' 카테고리의 다른 글
| [ISLP Chapter 10] Single/Multi Layer NN (0) | 2024.04.25 |
|---|---|
| [ISLP Chapter 9] 서포트 벡터 머신 (0) | 2024.04.22 |
| [ISLP Chapter 7] 조각별 다항식 회귀 (Piecewise polynomial regression) (0) | 2024.03.09 |
| [ISLP Chapter 7] 기저함수 (0) | 2024.03.06 |
| [ISLP Chapter 7] 계단함수 (0) | 2024.03.06 |