728x90
다항식 회귀모델에서는 데이터 전체(전역)에 대한 하나의 통합된 모델을 생성하였다. 하지만 이는 데이터의 다양한 패턴과 특징을 반영하는데에 한계가 있다. 따라서 계단함수를 사용하여 데이터의 구간(지역)을 나누어 각 구간마다 다르게 적합한다.
계단함수
① 절단점(cut point, c)을 사용하여 연속형 변수 -> 순서범주형 변수로 변환

* I( ) (지시함수, Indecator function) : X가 괄호 안의 범위에 해당하면 1, else 0을 반환한다.
- k개의 절단점을 사용하여 K+1개(C0 ~ CK)의 변수를 만들어낸다.
- C0 ~ CK를 모두 더하면 항상 1
- 각 지시함수가 1인 경우(True인 경우) 특정 상수 값으로 xi를 할당
② 최소제곱 적합
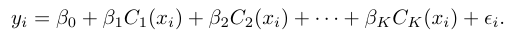
xi가 속하는 구간이 선택되고, 그 구간에 따른 상수를 부여한다. 각 구간별로 모델을 적합한다
=> 결론 : 각 구간마다 서로 다른 적합을 수행한다.
- X < c1 인 경우 yi = B0 로 모든 설명변수는 0이 된다. 이 경우 절편의 값만 상수로 남는다. 이것은 y에 대한 평균값이라고 할 수 있으며 X가 다른 구간에 포함된다면 yi = B0 + Bj 로 y의 평균 증가를 나타낸다.
* C0는 절편과 중복되기 때문에 제외한다
: k개의 절단점으로 K+1개의 구간을 나누어 순서범주형 변수로 변환했다. k개의 변수를 구분하기 위해서는 k-1개의 가변수가 필요하다. 따라서 C0를 제외하고 절편을 살린것이다. 제외할 CK는 임의로 정한것이며 C0를 제외하지 않고 절편을 제외하는 방법도 있다.
계단함수로 적합한 그래프 (실선은 최소제곱 적합선 점선은 95% 신뢰구간을 나타낸다)

- 왼쪽 그래프를 보면 모든 데이터를 통합적으로 적합하는 모델이 아닌 3개의 구간으로 나누어 각각에 대해 적합된 모습을 보인다.
- 왼쪽 그래프를 보면 약20~33세 구간에서는 산점도를 보면 양의 방향으로 증가하는 모습을 보이지만 최소제곱적합선에서는 이 구간이 하나의 상수로 표현되어있어 자연스러운 중단점(breakpoint, 데이터가 변화하는 지점이나 특정한 패턴이 나타나는 지점)이 없다면 실제 데이터의 특징을 잘 표현하지 못할수도 있다.
* 중단점(break point), 절단점(cut-off point)- 절단점(cut-off point) : 이진 분류나 이벤트의 발생 여부를 결정하기 위해 사용 (예시 : 확률이 절단점보다 크면 하나의 클래스로 분류되고, 작으면 다른 클래스로 분류)
- 사용자가 주어진 문제에 맞게 적절한 절단점과 중단점을 선택하여 모델을 구성
- 중단점(break point) : 계단함수에서 구간을 나누는 지점 - 오른쪽 그래프는 왼쪽 그래프보다 유연하여 더 많은 구간으로 구분되는 모습을 보인다. 65세 이상의 경우 신뢰구간이 급격히 넓어지는데 65세 이상의 wage 관측치가 적고 넓게 분포해있기 때문이다.
로지스틱 회귀에서 계단함수 적합

- 로지스틱 회귀도 로짓의 관점으로 선형 결합의 형태를 가짐
- age를 기반으로 wage > 250인 고소득층과 wage <= 250인 저소득층으로 분류 가능
- 오른쪽 그래프 : age를 기반으로 해당 데이터가 고소득자일 확률을 나타내는 그래프이다.
728x90
반응형
'통계 > ISLP' 카테고리의 다른 글
| [ISLP Chapter 7] 조각별 다항식 회귀 (Piecewise polynomial regression) (0) | 2024.03.09 |
|---|---|
| [ISLP Chapter 7] 기저함수 (0) | 2024.03.06 |
| [ISLP Chapter 7] 다항식 회귀 (0) | 2024.03.05 |
| [ISLP Chapter 4] 분류 (1) | 2024.02.13 |
| [ISLP Chapter 3] 선형회귀 (1) | 2024.01.27 |